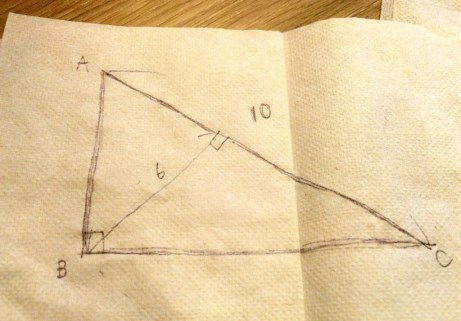
マイクロソフト入社試験「この三角形の面積を求めなさい」が理系男子もお手上げの難解トリック
天才というのは、我々と違う世界を見ているのではないだろうか? 私たちが「当たり前」と思っていることを疑問に感じ、それを論理的に説明づける……その繰り返しが科学の歴史だと言えるだろう。
いま、そんな天才しか解けないのではないか、という問題が話題となっている。 それはマイクロソフトの入社試験だというのだが、一見、小学生でも解けるレベル。
しかし、実際は理系男子もお手上げな超難問だというのだ。あなたには、このトリックが解けるだろうか?
マイクロソフトの入社試験
「誰か答えを教えて!」そうネットに書きこんだのは、インドの国立工科大学ワランガル校でコンピュータ理工学を学ぶパラシャントさんだ。彼の友人が、マイクロソフト社を受験し、最終選考まで進んだのだそう。 そこで、こんな難問を出されたのだという。
「この三角形の面積を求めよ」
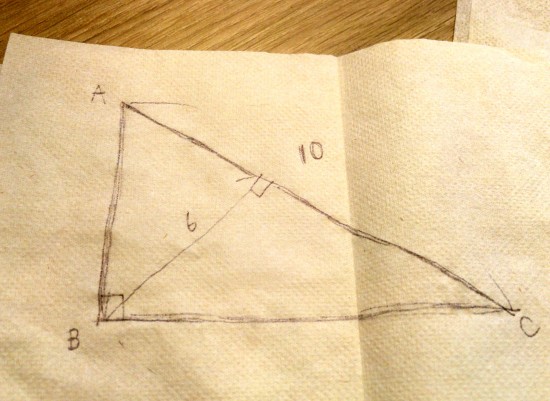
問題に登場するのは、ひとつの直角三角形だ。斜辺が “10”、90度角から斜辺に向かって伸びる 垂直線が “6” という三角形である。
小学生でも解けそうなんだけど……優秀な就活生に出すには、ちょっと簡単すぎない? やや疑問だが、パラシャントさんの友人は公式通り「10×6÷2=30」という答えを出したのだという。すると……。
「10×6÷2=30」じゃなかった!
まさかの不正解! いや、与えられた数字を使ったらどう考えても30だ。きっと100人中99人はそう答えるだろう。しかし、無慈悲にも不正解。不合格となってしまった。
面接官「そもそもこんな三角形は存在しない」
「10×6÷2=30」がダメなら、どう回答すれば良かったんだよ!? 友人は面接官に正解を尋ねたのだという。すると、こんな驚きの返答があったというのだ。
「そもそもこんな三角形は存在しないのです。考えればわかりますよ!」
は? 存在しない? 面積を求めよと言ったのはそちらでしょう? わけがわからないよ……! この面接官のヒントでひらめいただけでも天才だと思うのだが、皆さんはわかっただろうか?
※以下の部分はソース元にてご確認ください。
http://rocketnews24.com/2016/05/20/750185/
以下、2chの反応
底辺かける高さ割るに
はい、入社
こんなメンドクセー会社入りたくねー
>>3
これが解だな
面接官の声なきメッセージ
>>3
心配無用
おまえなんか最初の(棒
ヒント:二等辺三角形
突然出題されたらひっかかりそうだ 記事になってるからヒッカケに気がついたが
結局正解は何?
>>10
そんなのパッと思いつかないよ・・・
>>87
例えば子供に普通に出されたら気づかないと思う。でもMSの入社試験でまさか…と思えば結構気付くんじゃないかな?
>>10
すぐ分かるのはすごい
情報リテラシーが求められているんだな。与えられた情報(三角形の数字)を鵜呑みにせず、自分て検証してどこが間違っているかを調べる力を持っているかを確認するための試験。
直角三角形なら6がありえんて話ね
設問に6とかいた時点で
もはやただの一休さん要請試験だな。
この手の問題は無意味だとGoogleが結論出していてすでに馬鹿認定
してるってーのにww
ブラック企業「うっせーな、試験官が存在するって言ったら存在するんだよ!」
存在しない三角形の面積を求めさせるぐらいだから 入社したら出来もしない仕事を無理やりさせられるんだろうな
>>17
ありもしない高額な給料を提示されてたりしてw
空欄にしといたら合格だったんだろうか?
俺「そもそもこんな三角形は存在しない」
面接官「私はこの三角形の面積を求めよ、と質問したのだよ?」「存在するかしないかはどうでもいい」「はい失格」
>>20
普通それだよな
中学くらいまでの学校の先生なら、100%そういうだろうな
>>20
それやったらぶん殴るわ
>>20
「『求めよ』は命令であって質問ではない。」
次回の入社試験では、わたくしが虎を退治いたしますので屏風から・・・・と一休さん大集合になってしまうな
お前ら入社させないって合図だろ ブブ茶漬みたいなもんだw
どうせこの三角形の面積は求められないとか捻くれた問題なんだろーなと思ったらそうだった
これ存在しないと気づいてもそれをどう指摘するかが難しいな 絶対に逆らえない上の人が明らかに間違ってた時にどうするかも含めてのテストなのか?
>>1
トリックも何も,こんなもん普通に考えりゃ設問の不備を指摘させるのが
質問者の狙いってわかるじゃん。
あほか・・・
確かにそうだなw
しかし詐欺だw
マイクロソフトの試験だと考えたら裏を考えないとね
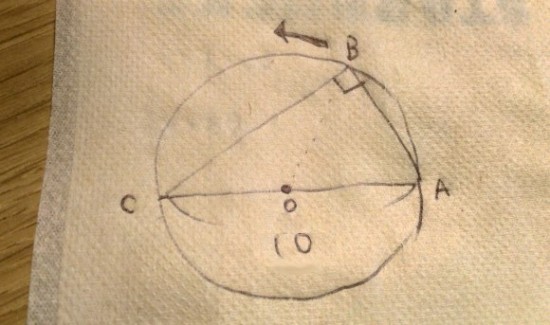
底辺を10とする直角三角形の高さの最大値は5
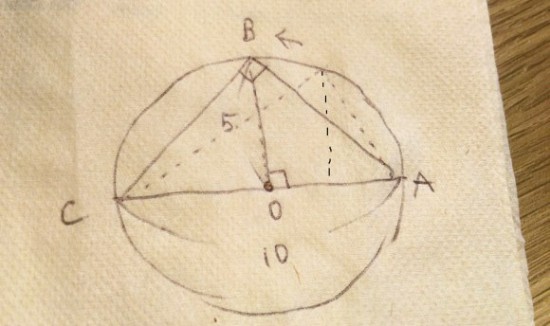
この絵に半径5の円を頭の中で瞬時に描けるかを問う問題 図形が頭の中でクルクルする人材でないとマイクロソフトには不要ということか?
>>48
やっとわかった。ありがとう。
円周角の問題と考えれば良かったんだな。日本の学校だとこういう指摘する生徒は先生に嫌われるから微妙だなー。
>>48
頭の中で図形をくるくる回さなくても,小学校で習う三角形の内角の和を知っていれば ありえないってわかる問題だよ。
この設問の条件を満たす三角形の形は,直角二等辺三角形だけ 長辺が10の直角二等辺三角形だったら垂線は5,よって垂線が6の三角形は存在しない。
問題として出されれば存在することを前提に計算するだろ。ちょっと簡単すぎるな、という違和感は感じるけど。とりあえず計算してしまうと思うな。
>>54
この三角形は存在しないという指摘がアリなのならば 面積を求めた上で角度が直角では無く間違ってるという指摘も正解にせざるを得ないはずだ
>>70
まず図形が手書きっていうのがな。
図形の問題って必ずしも忠実な形ではないっていうことも考慮してしまうからそのまま計算しちゃうよな。 図形そのものにケチを付ける発想はひょっとすると入社後に足を引っ張る人格になる可能性もある。 他の問題を解く時間的な計画もあるからちょっと意地悪すぎると思う。
>>102
プログラマーの検証的思考を問うのならば この問題のどこが間違ってる可能性があるのか全て列挙するとかかな
これならぐうの音も出ねーだろ
こういうので人を評価している気になってる連中って、特にコンサル系とかに多いよな。インチキが上手い奴を探しているって感じで。
そんな一休さんはどうでもいいからwindows10のアプデなんとかしろよ すげえ騒ぎになってんじゃねーか!
>>56
ほんとそれだわ
天才集めた結果があのゴリ押しなのかと
OSを強制アップグレードさせようとする クズの企業らしい入社試験ですね




この2chスレまとめへの反応
問題の是非はともかく…
解(=結論)へたどり着く手段は、何通りもあると思うよ
非ユークリッド空間ならこのような三角形も存在すると思って公式通りに計算しました
…という返答でどうだろうか
平面ではなく球体の上にならそんざできるとか言い返してたら合格とかありえたんかな
ACと垂線の交点をDとして、
あとは三平方の定理から方程式つくってAD^2-100AD+36=0が得られるだろ?
あとはb^2ac=100-34*36=-44 <0
これでACが実数で存在しない事になるから、こんな三角形は存在しない。
こんなところだろw
ただし「解なし」が最初からわかってたからこう計算できるんで
普通は底辺と高さで出しちゃうよなあw
「この三角形」という設問がウソなら、ウソつく会社ってことでw
そういやAPI(この会社の提供する部品)にもバグがあるしなぁw
※5
ウソではない
というか「この三角形」という前提があるから「解なし」が導けるんだ。
三角形という前提条件がなければ、値が負でも虚数解でもOKになっちゃうじゃん?
ところでこの図は何の紙に描かれているのだろう?
要するに“バグを見抜く力”を試してるんだろ。
世界最大のソフト会社らしい問題だよ。
※7
俺も最初に気になったw
ペーパーナプキンっぽいね
試験後にカフェでも寄ったんだと
いつからユークリッド幾何学の問題だと錯覚していた?
※2
球面上で成り立つんだけどその場合面積は30より大きくなるはず
その値まで計算するのが模範回答だと思う
おれは直角三角形だから一辺10の四角と仮定してみて6ってなんや???と思いつつ
10×10÷4で25が答えと思ってた
俺は中学卒業時に鑑別入っていた超ーアホやけど・・・
0.1秒でわかるで?
土方のアホやけど俺の周りでも「10×6÷2=30」こんなアホな事一瞬でも考える奴いねーよw
>きっと100人中99人はそう答えるだろう
俺より頭悪い奴が100人中99人もいるわけねーだろw
88が何言ってるのかマジで意味わからん