53: 2020/04/26(日) 21:38:34.740
1が本当だと仮定すると2と3は嘘だから1と2に車
2が本当だと仮定すると1と3は矛盾するから2は嘘
3が本当だと仮定すると1と2が嘘で少なくとも2に車
65: 2020/04/26(日) 21:41:28.262
>>53
3が本当のこと言ってる場合に3に車があるかどうかわからないから少なくとも2に車があって1には無いとしか言えないけど車の数は条件あるのかな
74: 2020/04/26(日) 21:44:20.471
>>65
問題文ちゃんと読んでみたら？
84: 2020/04/26(日) 21:47:34.906
>>74
「どれかに」ってのは車が入ってる箱は1つってことを言ってそうだけど2つや3つでもあるとは読めるのかな？ 日本語弱いからわからない
86: 2020/04/26(日) 21:48:14.227
>>84
えぇ……
91: 2020/04/26(日) 21:50:21.468
>>86
結局「どれかに」ってのは車が入っている箱は一つってこと？
83: 2020/04/26(日) 21:47:34.704
>>65
問題文読めない奴って絶対頭悪いわ
57: 2020/04/26(日) 21:40:03.019
国語やんけ
60: 2020/04/26(日) 21:40:18.555
2に入ってて3が本当のこと言ってる
車が入ってる箱が本当のこと言うわけじゃない
68: 2020/04/26(日) 21:42:16.550
これあれだろ
答えが複数になるのにドヤ顔で一つを挙げる奴を馬鹿にするやつだろ
79: 2020/04/26(日) 21:46:07.455
答えは少なくとも
①1が本当で1と2に車
②1が本当で1と2と3に車
③3が本当で2に車
④3が本当で2と3に車
ただ「どれかに車が入っている」って表現的に車は一つっぽいからその条件で言うと③の3が本当で2に車 が正解っぽいけどなんかフワッとしててしっくりこない
97: 2020/04/26(日) 21:55:48.305
>>79
いや違うぞ
車は複数あるかもしれないからどれもが正解の確率はある ただ100%正解なのは2ってだけ
99: 2020/04/26(日) 21:57:19.883
>>97
マジで！？
同じ意見の人いて安心した
80: 2020/04/26(日) 21:46:33.731
箱揺らしたほうがはやいわ
85: 2020/04/26(日) 21:47:48.117
正解見たけど納得いかん
▼仮説を立てて考えると簡単にわかりますよ！
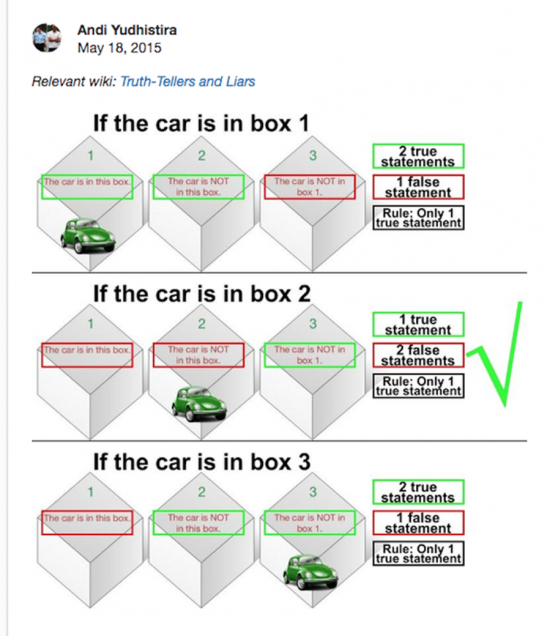
１に車が入っていると仮定した場合。
１と２が真実が書いてあることになってしまうので間違い。
2に車が入っていると仮定した場合。
１と２は真実ではなく、３だけが真実となるので、正しい。
３に車が入っていると仮定した場合。
１は真実ではない、２と３はどちらも真実になってしまっているので間違い。
以上の事から２に入っているという仮説が正しいので、正解は２の箱となります！こう考えると単純ですね！
皆さん分かりましたか？面白い問題でしたね。
https://fundo.jp/106359
82: 2020/04/26(日) 21:47:14.313
金属探知機もってこい
87: 2020/04/26(日) 21:49:00.841
1が本当 → 1○ 2○ 3(不明)
2が本当 →1と3の発言に矛盾が生じるのでこのような場合はありえない。
3が本当 →1× 2○ 3(不明)
2に車がはいってることだけは確実
90: 2020/04/26(日) 21:49:33.178
あー納得したわ
92: 2020/04/26(日) 21:50:26.818
2
論理的思考力の問題なのは分かるがこういうのが数学にカテゴライズされるのが何となく納得いかん 数A習ったときもこれ国語力の問題じゃね？って思ってた
95: 2020/04/26(日) 21:54:00.943
俺は「どれ」って言葉は単数で使うけど厳密には複数でも使えるとかだったら問題としてはそこまで考慮しないといけない気がして 要らぬ心配だったのかな
98: 2020/04/26(日) 21:56:17.037
問題理解するのに20秒かかったわ(´・ω・`)
113: 2020/04/26(日) 22:14:44.660
数学的センス関係ないよね
1が本当だとすると2にも車が入ってる3は不明
2が本当だとすると1と2には入ってないから3に入っている
3が本当だとすると1には入ってなくて2には入ってるので3は不明
問題に「いずれかの箱1つに」とかあれば3も確定できる
114: 2020/04/26(日) 22:17:26.311
>>113
マジでその文言ほしい
115: 2020/04/26(日) 22:17:53.719
>>113
すまんが2が本当ってのはあり得ないんだわ
だから2を選ぶのが正解
116: 2020/04/26(日) 22:18:10.057
>>113
2の発言が本当とした場合の考え方に誤りがあるよ
119: 2020/04/26(日) 22:22:55.900
>>116
そうだね2のケースは無いね
133: 2020/04/26(日) 22:43:12.726
問題文は、車が入っている箱と 本当の事を言っている箱がそれぞれ一つあると読める。
1の「この箱には車が入っています」が本当だとすると、「2の箱にも車が入っています」となる 矛盾
2が本当だとすると 1と3が両方嘘であることになるが、お互いに矛盾する
3が本当だとすると、1と2が嘘ということになるが、その場合2の箱に車が入っていることになり矛盾しない
135: 2020/04/26(日) 22:46:01.390
あたまわるいやつばっかりだな
段ボールに車が入るわけないだろ
137: 2020/04/26(日) 22:48:19.402
>>135
天才
139: 2020/04/26(日) 22:51:31.466
>>135
140: 2020/04/26(日) 22:52:01.368
>>139
なんだと…
この2chスレまとめへの反応
引用元URLを記載するっていうごく当たり前のこともできないの？
車は２台あって１，２に入っていて１が本当
車は３台あってすべてに入っていて１が本当
どれかに入ってるだから普通は入ってる箱は1つと考えるわ
本当のことを言っているのは「一つ」と、数が指定されているのに対し
車が入っている箱は「どれ」と、特に数の指定はされていない。
>>87 の回答は整合性がきちん取れており、この回答が正解と言える。
少なくとも問題の条件だけでは３の箱に入っているのか入っていないのかのどちらも取れる。
センスっていうか、何度かこういう問題問いてれば解き方のコツみたいなもんは誰でも会得できるような気がするんだが
※2
問題文も読めない激烈バカ発見w
本当の事言ってるのは一番右だけど、左から順番に検証してったら間に合わない罠
全部で8通りしかないけど
000 どこにも入ってないので偽
001 ２と３が成立するので偽
010 ３のみ成立するので真
011 ３のみ成立するので真
…
みたいに検証していくから20秒じゃ無理
車は1台に限定しないと20秒はキツイ
本当のことを言ってるのが３で確定で車が入っているのは２でも車が入っている箱が一つとは言ってないので３にも入っている可能性があるって感じちゃうけ？
別に「車が入っている箱を全て答えよ」って問じゃないんだから台数関係なく
１に入っていると仮定→１真３偽→真は一つだけという条件から２偽→２にも入っている
２に入っていると仮定→１偽２偽３真で条件満たす
３に入っていると仮定（無意味）→１と３のどちらかが真→真は一つだけという条件から２偽→２にも入っている
２には確実に車が入っているから「２」と答えればいい
※10
基本的に同じだと思うが、俺は車は1台で考えてしまったので、
１が本当なら２は嘘、すると２にも車が入っていることになるので1は嘘となる。
２が本当なら３は嘘、しかしの１の嘘と矛盾するので２は嘘となる。
で２に車が入っているという結論に。
、
１と３が完全に食い違っているから少なくとも２は真実を告げていない。イコール、２に入っている。最大限単純に考えるとここで回答が確定できる。
が、それ以外のロジックの成立パターンを見落としている可能性はあるから「設問自体が成立しない」ケースなどがあれば不正解になってしまう。そこの検証はしてない。（めんどくさい）
例として「絶対に成立しない三角形の図表を提示して面積を求める設問」の問題とかも出題としては実在するからね。
箱が三つある。そのどれかに車が入っている。
素直に解釈すれば「どれか一つに」車が入っているとなるわな。
二つ入っているのなら入っていない箱を当てさせる問題にするし、
三つ入っているのならそもそも問題にならないんだから。
てか元の問題は英文だったりしないのかな？
英文なら単数か複数はっきりわかるだろ。
原文あった
There are 3 boxes, exactly one of which has a car.
You can keep the car if you pick the corrent box.
On each box there is a statement, exactly one of which is true.
12.の通り
左と右は正反対の内容を述べている。
ゆえにどちらか一方が正しく、もう一方はうそ。
うその書き込みが2つあるので真ん中はうそ。
ゆえに「２」の箱に車が入っている。
1には確実に入っていない
2には確実に入っている
3はどちらの可能性もある
公務員試験でも「確実に言えるものはどれか」っていう問いがよく出るから、「3にも入っている可能性があるから3も正解」って言っている人は試験に落ちる
1が本当のことを言っている場合：
1にも入っているし、2にも入っている。
3には入っているかどうか分からない。
2が本当のことを言っている場合：
1と3の発言が矛盾するのでありえない。
3が本当のことを言っている場合：
1には入っていない。
2には入っている。
3には入っているかどうか分からない。
「確実に入っている」のは2。
ただし1にも3にも入っている可能性はある。
※14が示してくれた原文には「そのどれか1つだけに車が入っている」とあり
これなら解釈が分かれることもない
訳し方が悪かったね
>論理的思考力の問題なのは分かるがこういうのが数学にカテゴライズされるのが何となく納得いかん 数A習ったときもこれ国語力の問題じゃね？って思ってた
数学ってのは論理の学問なんだから言語能力も大事ってことわからんのかね
計算問題だけが数学だとでも思ってんのか