【悲報】このグラフを『見辛い』と感じる人は知的障害者である確率が高いらしい…

ただし、縦軸に目盛りが割り振りされていないことはノーカンってことで

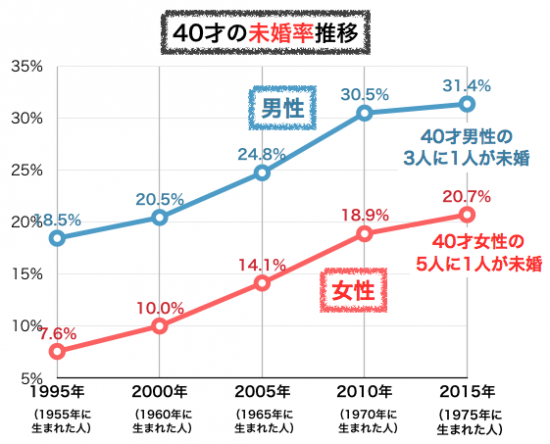
画像
http://2ch-matomenews.com/wp/wp-content/uploads/2023/10/X5dd9.png

【画像】日本人さん、『カーキ』がどんな色か分からない……………

http://2ch-matomenews.com/677633/

【花園衝撃】女子寮の華やかな生活がこちら【→画像】

http://2ch-matomenews.com/683215/

【最新版】「童貞をコロすセーター」の現在がこちら【→画像】

http://2ch-matomenews.com/685445/

【画像】インスタ女子さん、理解されない『性癖』を公開してしまう

http://2ch-matomenews.com/684484/

【悲報】点字ブロックさん、視覚障害者を天国へ誘導【画像】

http://2ch-matomenews.com/666977/

2: 2018/04/23(月) 08:52:57.47

大体の人間が知的障害者になりそう

3: 2018/04/23(月) 08:53:35.28

見辛いわ

4: 2018/04/23(月) 08:53:42.43

色使いのセンスが

47: 2018/04/23(月) 09:10:10.33

何がいいたいかはわかる

13: 2018/04/23(月) 08:56:53.93

週刊新潮の表紙かな

5: 2018/04/23(月) 08:53:51.57

総務省さんさぁ

6: 2018/04/23(月) 08:54:11.64

理解は出来るけど見辛いかどうかで言えば見辛いだろ

9: 2018/04/23(月) 08:54:48.51

色センスは微妙だけど見づらくはないやろ

10: 2018/04/23(月) 08:55:09.43

棒グラフでいい定期

11: 2018/04/23(月) 08:55:37.16

ぱっと見で分かるように作成してくれや

18: 2018/04/23(月) 08:58:14.26

まずこのグラフを採用したやつが知的障害やろ

21: 2018/04/23(月) 08:59:18.89

錯覚起こすからやっちゃダメなやつやで

28: 2018/04/23(月) 09:02:24.50

こういうグラフで大事なのは直感的なわかりやすさやからな、しばらく考えれば意味がわかりますじゃダメや 下手にこねくり回してわかりにくくするくらいなら最初から複数のグラフで比較すればええねん

40: 2018/04/23(月) 09:06:44.73

これは割合を表すものとしては妥当やけど色の主張が激しくて見づらいというところはある

46: 2018/04/23(月) 09:09:52.60

色盲に優しくねえな

【革命】オッパイ画像に『立体感』を持たせてみた →画像

http://2ch-matomenews.com/606977/

49: 2018/04/23(月) 09:10:34.16

一番大事な縦軸なくて草