
面接官「『0.99999999…』を『1』にするにはどうすればいいですか?」
1: 2018/10/29(月) 13:21:04.00
9: 2018/10/29(月) 13:22:07.43
ちょっと背中をおしてあげる
11: 2018/10/29(月) 13:22:15.80
まず大量の紙を用意します
14: 2018/10/29(月) 13:22:27.87
問題が完成度なら、0.999999あたりで見切り発車します
問題が可能性なら、1にはなりませんので見切り発車します
62: 2018/10/29(月) 13:30:01.39
はい!分かりません!
65: 2018/10/29(月) 13:30:15.31
些末なことを気にするのは凡人だけですな デュフフ
4: 2018/10/29(月) 13:21:44.83
同じ数で÷
8: 2018/10/29(月) 13:22:07.42
>>4
かしこい
16: 2018/10/29(月) 13:22:36.92
気合いです!
17: 2018/10/29(月) 13:22:39.53
四捨五入する
6: 2018/10/29(月) 13:21:50.39
ワイが加わることです
22: 2018/10/29(月) 13:23:18.59
>>6
戦力低すぎて草
25: 2018/10/29(月) 13:24:27.04
>>6
ほならアイも加わるわ
68: 2018/10/29(月) 13:30:31.27
>>6
限りなく0に近い戦力
15: 2018/10/29(月) 13:22:30.26
データを改ざんします
20: 2018/10/29(月) 13:23:08.36
元々同じです
21: 2018/10/29(月) 13:23:18.25
0かけて1足します!
52: 2018/10/29(月) 13:28:19.13
>>21
ワイはすき
割と上手いこと言えそう
23: 2018/10/29(月) 13:23:40.52
0乗にしたらええど
29: 2018/10/29(月) 13:25:03.21
その9はどこまで続いてますか?
36: 2018/10/29(月) 13:25:44.85
書き続けたらいつかは1になるらしい
38: 2018/10/29(月) 13:26:39.84
0.11111111…足せばええだけやん
47: 2018/10/29(月) 13:27:29.44
エクセルにぶち込む
49: 2018/10/29(月) 13:27:38.06
round関数使います
66: 2018/10/29(月) 13:30:24.18
定義するだけやぞ
67: 2018/10/29(月) 13:30:24.51
x=0.99999…
10x=9.99999…
10x-x=9x=9
x=1
34: 2018/10/29(月) 13:25:31.09
0.99999….=1定期
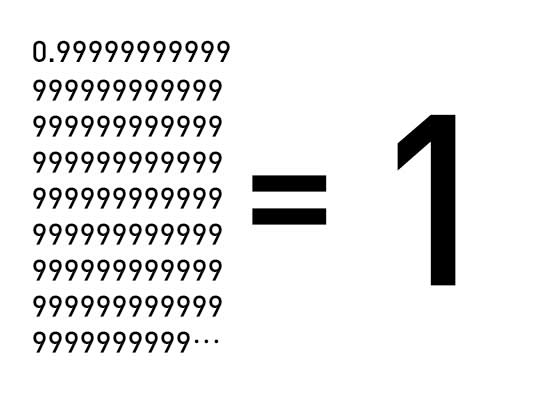










この2chスレまとめへの反応
四捨五入しとけ
00000円01銭を四捨五入しますねー
有効数字3桁で切ってしまえ
ルールの定義がされてないなら分数にして表せばええやん
0.999…=0.333…+0.666…=1/3+2/3=1
※
0.333…=1/3
0.666…=2/3
簡単。
1=1÷3×3
で、
1÷3=0.3333333・・・
3で割った答えに今度は3掛けると0.9999999・・・
よって、
1=0.9999999・・・
そのままでも1でいだろ?
イプシロンn論法
そこまで行くと受け手側の解釈次第なので、1とは認めない人の方の認識を変えさせます
有名な数学の雑学的証明問題やん。
0.999…÷3=0.333…=1/3
1/3×3=1
そんなの 0.99999999…と1との差分を 0.99999999…に加算してください
計算式で言うと
X=1-0.99999999…
として
0.99999999…+X=1になります
でいいよ
※5
それは1÷3の結果を「0.999・・・」と便宜上表記しているから見た目が同じになるだけで、純粋な「0.999・・・」という数値とは違うのだから間違ってる。
円周率πは3よりも大きく4よりも小さい。3.1よりも大きく3.2よりも小さい。3.14/3.15よりも3.141/3.142よりも3.1415/3.1416よりも3.14159/3.14160よりも…と、どこまで行っても少数で表記可能な近似値とπには明確に差がある。これと同じで、純粋な「0.999・・・」という数値は1よりも小さく0.9よりも大きい。少数で表記可能な近似値をどこまでいっても明確に差がある。
一方、1÷3の結果は少数で表記しようとすると純粋な「0.999・・・」と同じになるだけであって、それよりもわずかに大きい。
有効数字で打ち切って範囲内だからOKとするのは物理であって、0.999・・・と1と1.000・・・01が違うことを違いとして考えることを打ち切るのは全く論理的じゃないだろ
面接官に「0.99999999999999…㎝の線を描いてください」と言い
それを別の人に「この線は何センチですか?」と、聞いたら
「1センチ」と答えるでしょう
では、ダメかな、
既に1やん
技術屋なら解析精度をあげるしかない。
数学なら元の式が必要。
簡単だよ
1÷3を計算してもらう
するとたいていの奴が0.3333…と答える
1÷3=0.3333…
じゃここ↑は認めるんだね?と確認をする
相手が「うん」と答えたら両辺に3をかけて
1=0.9999…
とする(論破完了おしまい
つか俺だったら言ってる質問の意味が分かりませんね
1と0.99999…は表記が違うだけで同じ値ですから
例えば1-0.99999…を考えてくださいとこまで行っても0でしょう?
と答える
つか0.99999…問題なんかちょっと数学かじってる奴なら周回遅れの問題なんだが
読み取り誤差で1にします。
面接官がアホすぎる
アホにはアホらしい回答をしてやれ
0をかけて1を足せば、0.99999・・・だろうと1になるよ、ってな